What is Power Inverter?
Power in the topic of this article is used to qualify the inverter so as to differentiate it from a logic inverter. If not otherwise stated, anywhere I write 'inverter' in this article, I mean 'power inverter'. An inverter is a basic component of any independent power system that produces AC power from DC. Inverters convert DC power stored in batteries or from PV module into AC power to run conventional appliances. Another application of inverter is in the case of uninterruptible power supply where the inverter with the aid of 12V DC battery is able to generate up to 110/220VAC (in this article, we shall focus our discussion on 220V, 50Hz AC output) that can be used to power most house and office appliances depending on their power rating.
An inverter consists of the following: pulse generator (or oscillator), gate or base driver circuit (optional), power switch (semiconductor switches) and step-up transformer. The block diagram of an inverter is shown below.
(b)
Figure1 Block diagram of inverter
Pulse generator: This is the signal processing and control circuit that generates the logic-level control signals used to turn the power switch (semiconductor switches) ON and OFF. There are many different circuits that one can adopt and use as pulse generator or oscillator, in fact many ICs that need few external components to be connected are available in the market for use. Such ICs include but not limited to NE555, CD4047, SG3524. The output of this circuit is either sent to the power switch directly the or via the driver circuit for amplification before it is sent to the power switch as the case may be. Of course, the choice depends on the design and/or transistors used as power switch.
Driver circuit: This circuit amplifies the signal from pulse generator to levels required by the power switch and provides electrical isolation when required between the power switch and the logic level signal processing circuit (pulse generator)
Power switch: Semiconductors like power transistors (Bipolar Junction Transistors or Metal-Oxide Semiconductor Field-Effect Transistors) and thyristors are used here as switching devices. They should be sized to withstand the high current of the primary winding (low voltage side) of the transformer.
Transformer: Transformers are of various types: step up, step down, autotransformer etc. They comprise of primary and secondary windings which may or may not be isolated from each other. The windings are electrically interlinked by a common magnetic circuit and operate based on the principle of electromagnetic induction. The number of turns of primary and secondary winding is related to their voltages and currents with the following equations.
Where,
N1 = Number of turns of the primary
N2 = Number of turns of the secondary
V1 = Primary voltage
V2 = Secondary voltage
I1 = Primary current
I2 = Secondary current
The size of transformer is proportional to its power. For an ideal (lossless) transformer, the input power equals the output power; but in practice, there is no lossless transformer.
Inverter Output Wave-form
One of the things one has to put into consideration when designing every components of inverter; of course any electrical or electronics system is the out. In the case of inverter, we have to put into consideration output wave-form in terms of peak and RMS values, and power output. For now, let us put power output aside as we shall discuss that later in this article.In conventional AC power system, the output wave-form is pure sine-wave as shown in figure 2 below. The relationship between the peak and RSM value of pure sine-wave is given by
OR
Where,
VP = Peak voltage
VRMS = RMS or effective voltage
IP = Peak current
IRMS = RMS or effective current
RMS is the root mean square or effective value of an alternating current. It is equivalent to steady DC current which gives the same amount of heat when flows through a given circuit for a given time as thus AC.
The above equation was not brought from heaven but a derived equation from the interpretation of RMS ( i.e, square Root of Mean of the Square value) using standard equation of sinusoidal alternating current (AC),
ORVP = Peak voltage
VRMS = RMS or effective voltage
IP = Peak current
IRMS = RMS or effective current
RMS is the root mean square or effective value of an alternating current. It is equivalent to steady DC current which gives the same amount of heat when flows through a given circuit for a given time as thus AC.
The above equation was not brought from heaven but a derived equation from the interpretation of RMS ( i.e, square Root of Mean of the Square value) using standard equation of sinusoidal alternating current (AC),
Figure2 pure sine-wave
Let us stop sine-wave at this junction since the inverter output is not sine-wave but square-wave as it is not easy to generate sine-wave from DC. We would talk more on square-wave. Wave-form shown in figure 3 was the output of my first inverter. I have designed, built and been using it since 2005 and still working perfectly. Nevertheless, there is a problem with the inverter and the problem is actually with the peak voltage of the output wave-form. The wave-form as shown in figure 3 below has peak value equal to RMS value. As I designed it for RMS voltage of 220V, the peak voltage also equal to 220V, hence some appliances that operate on DC voltage from AC supply may not work. Check my 12V regulated DC power supply to see how I have used peak voltage to determine the voltage applied to LM7812 (voltage regulator IC). This problem was not thought of until I tried to used it with my desktop computer and it was not coming on. I sat back and checked my design very well, I could not fish out the problem until after some months. The problem was quite inexperience as I was so much in hurry to design and build an inverter for my use and by myself without putting into consideration all necessary things. As I said earlier, it is still working perfectly except that my desktop computer (other appliances I use at home work with it) that does not work with it. Of course my laptop works perfectly with it.

Figure3 square-wave
This problem leads to introduction of what is called modified sine-wave as shown in figure 4. In this wave-form, the peak value is designed to equal to the peak of sinusoidal voltage that will give the same RMS voltage for which the inverter is being designed. As you can see in figure 4, there is clearance in-between two half cycles. This is called duty cycle. Duty cycle that will give peak and RMS value that equal to that of sine-wave is 25% of period of a complete oscillation. Don't worry, I will use a simple mathematics to show you how I came about this.

Figure 4, modified sine-wave
Figure 5, modified sine-wave showing duty cycle x, half period (cycle) y and complete period (cycle) t, Peak voltage VP and rms voltage VRMS
From figure 5,
Therefore, pulse duration
I want you to follow how I will use 'square Root of Mean of the Square value'Square value
Therefore, Mean of the Square value of a complete cycle (2 halve cycle)
square Root of Mean of the Square value
If we square both sides, the above equation becomes
By multiplying both sides by t, we are left with
Now let us divide both sides by 2(VP)2
By collecting like terms
Therefore duty cycle (x)
i.e, 25% of period t of a complete cycle.
That is the frequency of the inverter.You don't have to be too worry if you don't understand that mathematical illustration. It is not even needed in the design of inverter as I only used it to show you how I arrived at 25% so that in future when I mention duty cycle you understand it and its significant.
The second stage is only identified with modified sine-wave inverter. This is when all switches are opened. This is shown in figure 7 when no current flows as all the switches are opened. This is called duty cycle and occurs in-between two halves and last for 5ms in the case of modified sine-wave inverter with duty cycle of 25% discussed earlier in this article.
Third stage of the cycle occurs when switches SW2 and SW3 are closed while SW1 and SW4 opened and current flows through the load from B to A (just opposite of what happen in the first stage) in the direction shown in figure 8 with the arrows. This also last for 5ms.
Last stage of the cycle is just the repetition of the second stage when all the switches are opened and no current flows. As I said earlier, it only occurs in modified sine wave inverter. The stages are repeated continuously until the inverter is turned off.
The duration of each of the four stages is 5ms; this implies that a complete cycle will last for 20ms. That is, the period t is 20ms
Since period t = 1/f; where f is the frequency of the AC voltage we want to achieve
Mode of operation
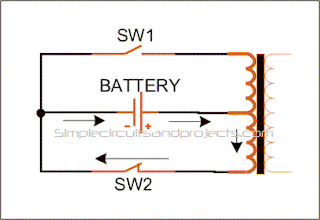
Figure 6, 7 and 8 bellow will be used to describe mode of operation of an inverter. When I said mode of operation, I mean process of converting DC voltage to AC voltage. Let's start from figure 6 which is the first stage; switches SW1 and SW4 are closed while SW2 and SW3 are opened. This makes current to flow in the direction shown with the arrows. These operation last for just 5ms in 50Hz modified sine-wave inverter with duty cycle of 25% (discussed above) and 10ms in the case of inverter with square-wave shown in figure 3 above. I want you to take note of the direction through which current flows through the load during this half cycle (A to B).The second stage is only identified with modified sine-wave inverter. This is when all switches are opened. This is shown in figure 7 when no current flows as all the switches are opened. This is called duty cycle and occurs in-between two halves and last for 5ms in the case of modified sine-wave inverter with duty cycle of 25% discussed earlier in this article.
Third stage of the cycle occurs when switches SW2 and SW3 are closed while SW1 and SW4 opened and current flows through the load from B to A (just opposite of what happen in the first stage) in the direction shown in figure 8 with the arrows. This also last for 5ms.
Last stage of the cycle is just the repetition of the second stage when all the switches are opened and no current flows. As I said earlier, it only occurs in modified sine wave inverter. The stages are repeated continuously until the inverter is turned off.
The duration of each of the four stages is 5ms; this implies that a complete cycle will last for 20ms. That is, the period t is 20ms
Since period t = 1/f; where f is the frequency of the AC voltage we want to achieve
If you are designing an inverter just like what I called my first inverter of the output wave-form as in figure 3, second and the last stages will not be there. However, first and third stages will have duration of 10ms each giving total of 20ms for a complete cycle just like the modified sine-wave above.
Figure 6, first stage of the process of converting DC voltage to AC
Figure 7, second and last stage (in modified sine-wave) of the process of converting DC voltage to AC
Figure 8, third stage of the process of converting DC voltage to AC
The process discussed above is a bridge type inverter. AC voltage is achieved just like that: without transformer. Application of transformer in the method depends on the battery voltage and desired AC voltage output.
Another method which I will quickly discuss is the use of two switches and transformer with center tapped primary winding. This is the method commonly found in inverter. Figure 9, 10 and 11 show the arrangement and the process involved.
voltage to AC using center tapped primary winding
transformer
Figure 10, second and last stage (in modified sine-wave) of the process of converting DC voltage to AC using center tapped primary winding transformer
Figure 11, third stage of the process of converting DC voltage to AC using center tapped primary winding transformer
I have used switches to discuss process of converting DC voltage to AC in inverter to let you have clearer picture of what transpires. When I mentioned switches, I know many of you will probably think of those wall switches in our houses. You are not too wrong anyway because 'switch is switch', but different switches for different purposes. Before now, electromagnetic switches that operated like a door bell were used for this purpose. Today, solid state electronic switches like BJT, MosFet, thyristor are employed. The use of electronic switches eliminates the unpleasant noise generated by those electromagnetic switches of those days, and also makes control of switching easy.
Use the formula:
and I have used switches to discuss process of converting DC voltage to AC in inverter to let you have clearer picture of what transpires. When I mentioned switches, I know many of you will probably think of those wall switches in our houses. You are not too wrong anyway because 'switch is switch', but different switches for different purposes. Before now, electromagnetic switches that operated like a door bell were used for this purpose. Today, solid state electronic switches like BJT, MosFet, thyristor are employed. The use of electronic switches eliminates the unpleasant noise generated by those electromagnetic switches of those days, and also makes control of switching easy.
Sizing of Various Components of Inverter
I said it earlier that when designing any electrical or electronics system, the output is always the focus of the design. Therefore I will start my design from the outermost component.Output socket/connector and Switch-over relay(optional)
Switch-over relay is used if you are designing your inverter to be interconnected with your utility supply. It switches over from inverter output to utility, vice versa automatically as the case may be depending on your design. Don't worry, I will still tell you more on this in my inverter circuits.Use the formula:
Where,
P is the power capacity of the inverter you are designing
V is the output voltage (the RMS voltage)
I is the output current (the RMS current)
Your output socket/connector and switch-over relay should be rated with current above the calculated value I above. Don't be too worried about RMS: this is the voltage or current your meter reads and displays when you measure voltage directly from the wall socket or your current using clamp-on meter or ammeter. Next is the transformer.
Input power therefore equals
P is the power capacity of the inverter you are designing
V is the output voltage (the RMS voltage)
I is the output current (the RMS current)
Your output socket/connector and switch-over relay should be rated with current above the calculated value I above. Don't be too worried about RMS: this is the voltage or current your meter reads and displays when you measure voltage directly from the wall socket or your current using clamp-on meter or ammeter. Next is the transformer.
Transformer
Primary and secondary winding current calculation
First, we assume the worst case of efficiency of 80%Input power therefore equals
The secondary winding current, IRMS
My preferred type of inverter is the one with center tapped primary winding transformer described above with figure 9-11. The reasons are simple: simplicity in switches arrangement and reduced current in each half of the primary winding. With my choice of center tapped primary winding transformer, half cycle current will only flow in each of the half winding. Current through each of the winding is given by:
Primary winding for inverter with square-wave in figure 3,
Where,Irms is the effective current flowing through the primary windingsImax is the total current delivered by the battery for a complete cycle.Note: the use of lower case letter 'rms' is to differentiate primary rms values from secondary. Please let us stick to this convention in this article.
Vbattery is the voltage of the battery for which you are designing your inverter. e.g. 12V, 24V, 48V…
Therefore,
Therefore,
For inverter with modified sine-wave in figure 4,
Therefore,
Wire gauge selection
Wire gauge is chosen base on the chosen current density of your design. Current density is the circular-mils per ampere of the insulated copper wire. It is chosen base on different conditions like: application (types of transformer), ease of heat dissipation and so on. For most transformer designed in conventional way, using the standard design rules for insulation, and having reasonable efficiency and safe temperature rise, the wire is commonly run at current density in the approximate range of 500 to 1000 circular-mils per ampere.
Now multiply your calculated currents (primary and secondary) above by the current density to get their correspondent circular-mils. Then check your wire table- published in many reference books and in manufacturers’ literature, to select the appropriate wire AWG for your windings. One of such tables can be found at http://en.wikipedia.org
Now multiply your calculated currents (primary and secondary) above by the current density to get their correspondent circular-mils. Then check your wire table- published in many reference books and in manufacturers’ literature, to select the appropriate wire AWG for your windings. One of such tables can be found at http://en.wikipedia.org
Core geometric
Figure 12, E-I type laminated iron core
i, j,k and l are all in inches
Window (W) = i x j
Cross sectional area (a) = k x l
Silicon iron is the most common transformer core either as junks or new in the market and it has flux density, B of 13000gauss. Power is related to Wa of the core by formula below.
Therefore, Wa (inch-cube)i, j,k and l are all in inches
Window (W) = i x j
Cross sectional area (a) = k x l
Silicon iron is the most common transformer core either as junks or new in the market and it has flux density, B of 13000gauss. Power is related to Wa of the core by formula below.
F = 1 for square waveform.F is the ratio of rms to average value. For modified sine-wave with duty cycle of 25%, F is 1.414. Therefore for modified sine-wave, Wa (inch-cube)
So while selecting your core in the market, look for one with core geometric (i.e, Wa product) that will give you the desired power for your inverter.
Number of turns
Using the basic transformer design equation:Primary turns (square-wave: F = 1, V - Vbattery)
Primary turns (modified sine-wave: F = 1, V - Vbattery)
Each half of the primary windings is
Secondary turns N2
Switches
You may wonder why I keep referring those transistors as switches. Yeah they do exactly what switches do. They are MosFets, bipolar junction transistors (BJT) and thyristors (silicon control rectifier). Though thyristors can deliver very high current and are used for high power inverter, its switching circuitry is complex. MosFets and BJT are two switches that I have used in my designs, but mostly MosFets. MosFets allow higher current than BJT. Unlike BJT which is current driven MosFet is voltage controlled, hence lesser power in the driver circuit.The drain-source (MosFet) or collector-emitter (BJT) current is the effective current of the primary windings. Therefore transistor with drain-source or collector-emitter current far above the effective current should be chosen. In a case where the current is several hundreds of ampere and one cannot get a single transistor that can deliver this current, multiple transistors of the same type will be used. The transistors will be connected in parallel such that the current spread across them equally. For instance, if the current is 100ampere and the available transistor can deliver 30ampere, four or more of the transistor should be used. It is always advisable to use transistor with drain-source or collector-emitter far above the effective current in application like this.
Oscillator/driver
I intentionally put the two together as there is no much as far as design of inverter is concerned. The driver can actually be omitted if not needed. As I explained above driver is introduced when oscillator is not given us the required voltage level needed to drive Mosfets or current that is enough to fire the BJTs to deliver required collector-emitter current. It is nothing but an amplifier circuit.Free multivibrator circuits are available online and in various electronic textbook that you can make use of. My preferred multivibrators are those ICs; what I did was surfing internet for data sheets of different multivibrator ICs. Of course all you need is in the data sheet only for you to make little adjustment/modification that will make it fits in to your design. What you need to do most of the time is to calculate frequency determining components of the circuit as it is presented in the data sheet.
Battery
The common battery used in inverter is a lead-acid battery of the type used in automobiles, sized to operate for few hours. Automotive batteries are often used because they are relatively inexpensive. Ideally, inverter should use deep cycle lead-acid batteries that have thicker plates and more electrolyte reserves than automotive batteries and allow for deep discharge without seriously reducing the life of the battery or causing damage to it. In a well designed inverter, deep cycle batteries can last up to ten years.In a case where deep cycle battery is not available for use, truck batteries can be used. They have thicker plates than car batteries, almost of the same thickness as deep cycle batteries. This will extend the battery life in an inverter significantly compared to a car battery.
Battery size calculation and specification
Batteries are rated in ampere-hour (Ah) and the sizing depends on your need: on how long you want the inverter to work relative to the loads you place on it. The formula below gives you the required battery size.
Discharge capacity arise from the fact that one does not use complete battery capacity. Only certain percentage (discharge capacity) of the battery would be used. A deep-cycle battery can be discharged up to 80% (actual value depends on your low voltage disconnect) of its capacity.












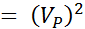




















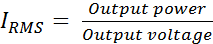















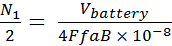








No comments:
Post a Comment